Se ha descubierto una ecuación matemática innovadora que podría transformar los procedimientos médicos, la extracción de gas natural y la producción de envases de plástico en el futuro.
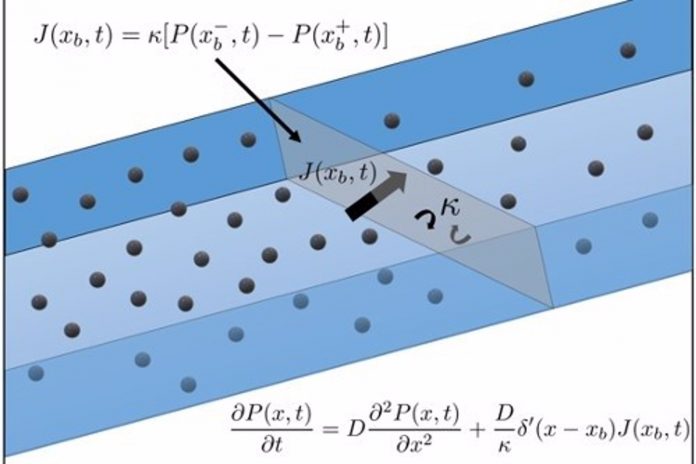
La nueva ecuación, desarrollada por científicos de la Universidad de Bristol, indica por primera vez que el movimiento de difusión a través del material permeable se puede modelar exactamente.
Llega un siglo después de que los físicos líderes mundiales Albert Einstein y Marian von Smoluchowski derivaran la primera ecuación de difusión, y marca un progreso importante en la representación del movimiento para una amplia gama de entidades, desde partículas microscópicas y organismos naturales hasta dispositivos hechos por ser humano.
Hasta ahora, los científicos que observaban el movimiento de partículas a través de materiales porosos, como tejidos biológicos, polímeros, diversas rocas y esponjas, tenían que basarse en aproximaciones o perspectivas incompletas.
Los hallazgos, publicados en la revista Physical Review Research, brindan una técnica novedosa que presenta oportunidades interesantes en una amplia gama de entornos que incluyen la salud, la energía y la industria alimentaria.
El autor principal Toby Kay, doctorando en Ingeniería Matemática, dijo en un comunicado: «Esto marca un paso fundamental desde los estudios de Einstein y Smoluchowski sobre difusión. Revoluciona el modelado de entidades de difusión a través de medios complejos de todas las escalas, desde componentes celulares y compuestos geológicos hasta hábitats ambientales».
«Anteriormente, los intentos matemáticos de representar el movimiento a través de entornos dispersos con objetos que obstaculizan el movimiento, conocidos como barreras permeables, han sido limitados. Al resolver este problema, estamos allanando el camino para avances emocionantes en muchos sectores diferentes porque las barreras permeables se encuentran rutinariamente por animales, organismos celulares y humanos».
La creatividad en matemáticas toma diferentes formas y una de ellas es la conexión entre diferentes niveles de descripción de un fenómeno. En este caso, al representar el movimiento aleatorio de forma microscópica y luego alejar el zoom para describir el proceso macroscópicamente, fue posible encontrar la nueva ecuación.
Se necesita más investigación para aplicar esta herramienta matemática a aplicaciones experimentales, lo que podría mejorar los productos y servicios. Por ejemplo, ser capaz de modelar con precisión la difusión de moléculas de agua a través del tejido biológico mejorará la interpretación de las lecturas de MRI (imágenes por resonancia magnética) ponderadas por difusión.
También podría ofrecer una representación más precisa de la propagación del aire a través de los materiales de envasado de alimentos, lo que ayuda a determinar la vida útil y el riesgo de contaminación. Además, cuantificar el comportamiento de los animales en busca de alimento que interactúan con barreras macroscópicas, como cercas y caminos, podría proporcionar mejores predicciones sobre las consecuencias del cambio climático con fines de conservación.
El uso de geolocalizadores, teléfonos móviles y otros sensores ha visto la revolución del seguimiento generar datos de movimiento en cantidad y calidad cada vez mayores en los últimos 20 años. Esto ha resaltado la necesidad de herramientas de modelado más sofisticadas para representar el movimiento de entidades de gran alcance en su entorno, desde organismos naturales hasta dispositivos hechos por el hombre.
El autor principal, Luca Giuggioli, profesor asociado de Ciencias de la Complejidad en la Universidad de Bristol, dijo: «Esta nueva ecuación fundamental es otro ejemplo de la importancia de construir herramientas y técnicas para representar la difusión cuando el espacio es heterogéneo; es decir, cuando el el entorno cambia de un lugar a otro.
Con información de El Nacional